다익스트라 최단 경로 알고리즘은 그래프에서 여러 개의 노드가 있을 때, 특정한 노드에서 출발하여 다른 노드로 가는 각각의 최단 경로를 구해주는 알고리즘이다.
- 기본적으로 그리디 알고리즘으로 분류됨 -> 매번 '가장 비용이 적은 노드'를 선택해서 임의의 과정 반복
- 알고리즘의 원리
- 출발 노드를 설정한다.
- 최단 거리 테이블을 초기화한다.
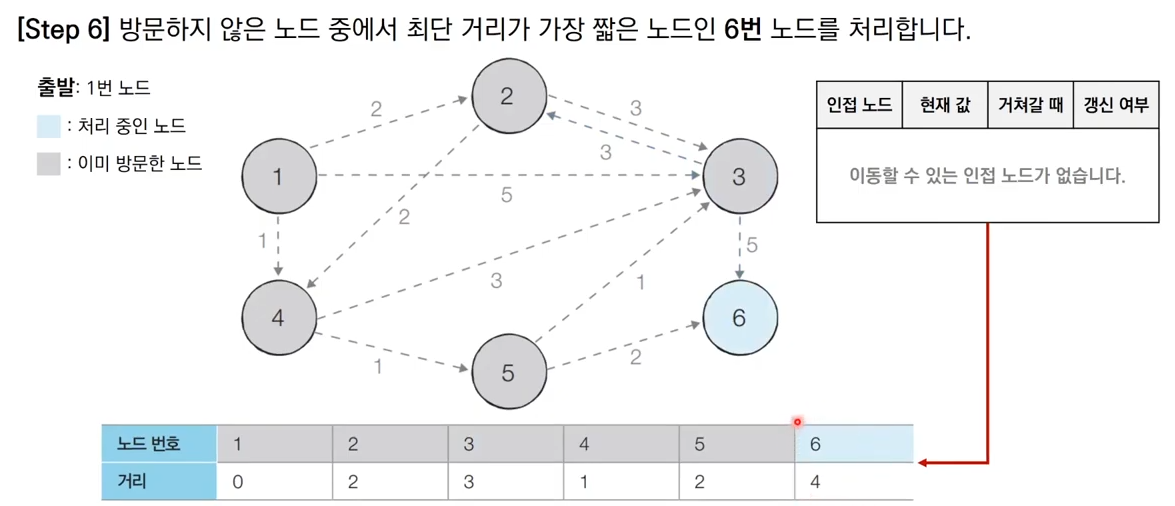
- 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택한다.
- 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다.
- 위 과정에서
3과4번을 반복한다.
그림으로 이해하는 다익스트라 알고리즘
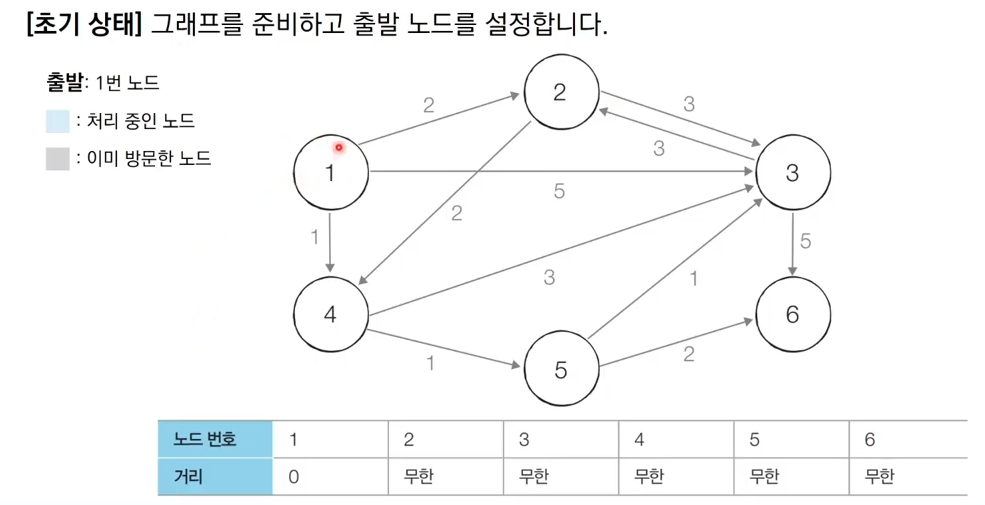

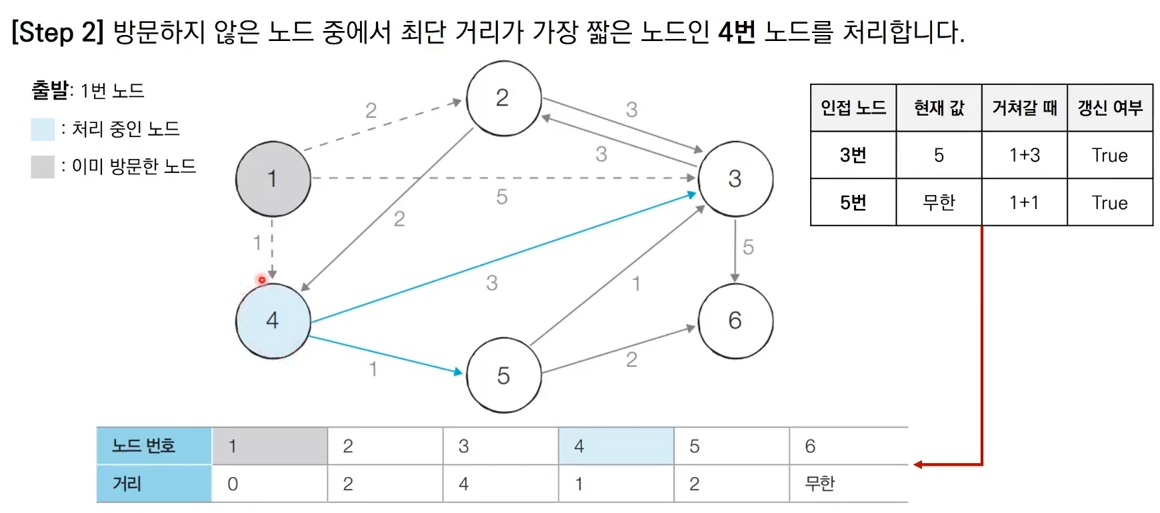
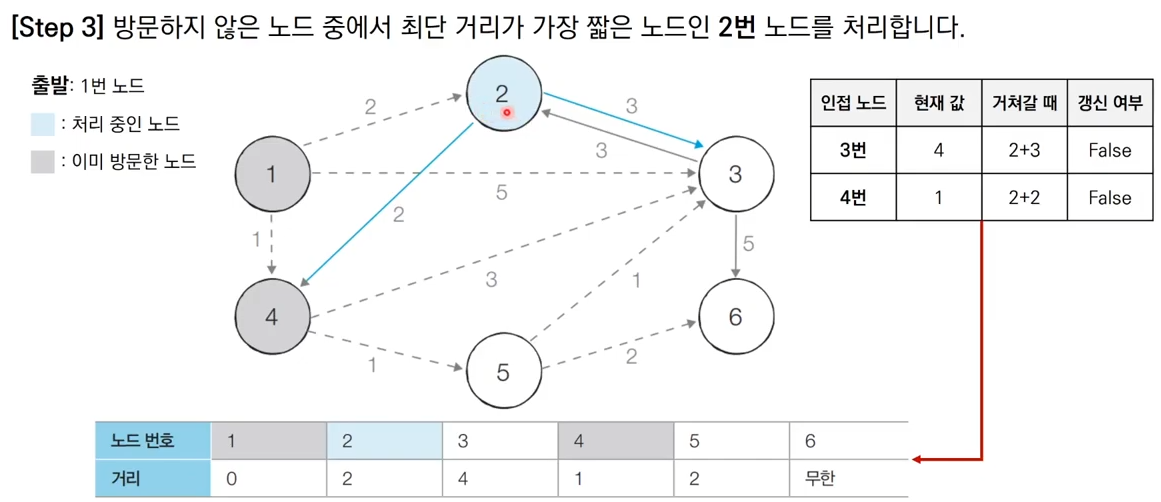

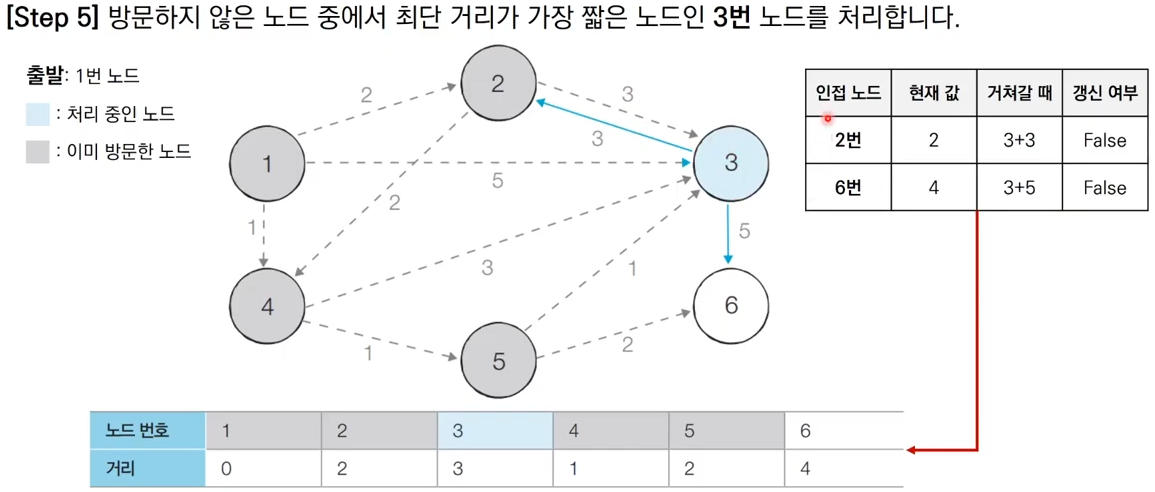
출처 : https://www.youtube.com/watch?v=F-tkqjUiik0
방법 1. 구현하기 쉽지만 느리게 동작하는 코드
시간 복잡도는 O(V^2)
# dijkstra - visted와 최단 거리가 짧은 노드 반환 구현 이용
graph = [[], [(1,2,4), (1,4,6)], [(2,1,3), (2,3,7)], [(3,1,5),(3,4,4)], [(4,3,2)]]
def dijkstra(start):
distance = np.array([INF] * len(graph))
visited = np.array([False] * len(graph))
# 시작 노드에 대해 초기화
distance[start] = 0
visited[start] = True
for j in graph[start]:
distance[j[1]] = j[2]
# 시작 노드 제외 n-1 노드에 대해 반복
for i in range(len(graph) - 1):
now = get_min_distance(distance, visited)
visited[now] = True
# 현재 노드와 연결된 다른 노드 확인
for j in graph[now]:
cost = distance[now] + j[2]
if cost < distance[j[1]]:
distance[j[1]] = cost
return distance[1:]
# 방문하지 않은 노드 중에서, 가장 최단 거리가 짧은 노드의 번호 반환
def get_min_distance(distance, visited):
return np.where(distance == min(distance[[not i for i in visited]]))[0][0]
for i in range(1, len(graph)):
print(f"{i}번 노드 : {dijkstra(i)}")
# 1번 노드 : [0. 4. 8. 6.]
# 2번 노드 : [3. 0. 7. 9.]
# 3번 노드 : [5. 9. 0. 4.]
# 4번 노드 : [ 7. 11. 2. 0.]np.where은 tuple로 반환함 [0] 접근 array[0]
방법 2. 힙을 이용한 개선된 다익스트라 알고리즘
최단 거리가 가장 짧은 노드를 선택하는 과정을 우선순위 큐를 이용하여 대체.
( 위의 get_min_distance() 함수에서 저는 np로 구현했지만, list로 할 시 모든 index 탐색하는 과정을 큐로 대체 )
시간 복잡도 O(ElogV)
- 쉽게 구현 하는 방법
- 출발 노드 푸쉬 후 거리 설정
- 큐가 빌때까지 팝(최단 거리가 짧은 노드)
- 현재 노드 거리와 거리 그래프중 최소값으로 설정
- 인접한 노드를 확인하면서 거리 그래프 업데이트하는 경우 그 노드 푸시
# dijkstra
import heapq as hq
graph = [[], [(1,2,4), (1,4,6)], [(2,1,3), (2,3,7)], [(3,1,5),(3,4,4)], [(4,3,2)]]
def dijkstra(start):
distance = np.array([INF] * len(graph))
# 시작 노드에 대해 초기화
distance[start] = 0
q = []
hq.heappush(q, (0, start))
while q:
dist, now = hq.heappop(q)
# 방문 여부 확인
if dist > distance[now]:
continue
for i in graph[now]:
# cost는 start 기준 거리 총합 -> 최단 거리 일 때 distance update하고 그 노드 push
cost = dist + i[2]
if cost < distance[i[1]]:
distance[i[1]] = cost
hq.heappush(q, (cost, i[1]))
return distance[1:]
for i in range(1, len(graph)):
print(f"{i}번 노드 : {dijkstra(i)}")
# 1번 노드 : [0. 4. 8. 6.]
# 2번 노드 : [3. 0. 7. 9.]
# 3번 노드 : [5. 9. 0. 4.]
# 4번 노드 : [ 7. 11. 2. 0.]다 하고 검토해보았는데 graph 작성 시 출발 노드는 index로 알 수 있으니 작성 할 필요없네요.
잘 배웠습니다 !
+ 플로이드 워셜 알고리즘
- 모든 지점에서 다른 모든 지점까지 구할 때
- 다이나믹 프로그래밍
- 점화식이 간단해서 간단하게 구현 가능
- 시간 복잡도 O(N^3)
# 플로이드 워셜 INF = 1e9 input_ = [[], [(2,4), (4,6)], [(1,3), (3,7)], [(1,5),(4,4)], [(3,2)]] n = len(input_) - 1 graph = [[INF] * (n + 1) for _ in range(n+1)] # 자기 자신에서 자신은 0 for a in range(1, n+1): for b in range(1, n+1): if a == b: graph[a][a] = 0 i = 0 for m in input_: for a, b in m: graph[i][a] = b i+=1 # k를 거쳐가는 경우 for k in range(1, n+1): for a in range(1, n+1): for b in range(1, n+1): # 플로이드 워셜 알고리즘 점화식 graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b]) graph = np.array(graph)[1:,1:].astype(int).tolist() print(graph) # [[0, 4, 8, 6], [3, 0, 7, 9], [5, 9, 0, 4], [7, 11, 2, 0]]
'자료구조와 알고리즘' 카테고리의 다른 글
| 냅색(knapsack) 알고리즘 (0) | 2022.02.14 |
|---|---|
| [python] 힙 구조 모듈 heapq (0) | 2022.01.06 |
| 자료구조와 알고리즘 (0) | 2022.01.06 |
| [python] 너비우선탐색, 깊이우선탐색(bfs, dfs) (0) | 2022.01.05 |


