본문 바로가기

부스트캠프 AI Tech/AI_Math

 (8)
[08] 베이즈 통계학 조건부 확률 베이즈 통계학의 이해를 위해서는 조건부확률 개념 이해 필요 $$ P(A \cap B) = P(B)P(A|B) $$ 조건부확률 $P(A | B)$는 사건 B가 일어난 상황에서 사건 A가 발생할 확률 $$ P(A|B) = \frac{P(A \cap B)}{P(B)} $$ $P(A|B)$는 A given B 베이즈 정리는 조건부확률을 이용해 정보를 갱신하는 방법 $$ P(A \cap B) = P(B)P(A|B) $$ $$ P(B|A) = \frac{P(A \cap B)}{P(A)} = P(B) \frac{P(A|B)}{P(A)} $$ A라는 새로운 정보가 주어졌을 때, $P(B)$로부터 $P(B|A)$를 계산하는 방법 제공 베이즈 정리 $$ P(\theta | \mathcal{D}) = P(\th..
[07] 통계학 모수 (parameter) 통계적 모델링은 적절한 가정 위에서 확률분포를 추정(inference) 하는 것이 목표이며, 기계학습과 통계학이 공통적으로 추구하는 목표 분포의 종류 매우 다양 → 어떤 확률분포를 사용해 모델링하지? 그러나 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알아낸다는 것은 불가능하므로, 근사적으로 확률분포를 추정(예측)할 수 밖에 없다 예측모형의 목적은 분포를 정확하게 맞추는 것보다 데이터와 추정 방법의 불확실성을 고려해 위험을 최소화 하는 것 데이터가 특정 확률분포를 따른다고 선험적으로(a priori) 가정한 후 그 분포를 결정하는 모수(parameter)를 추정하는 방법을 모수적(parametric) 방법론이라고 한다 특정 확률분포를 가정하지 않고 데이터에 따라 모..
[06] 확률론 딥러닝에서의 확률론 딥러닝은 확률론 기반 기계학습 이론에 바탕을 두고 있다 기계학습에서 사용되는 손실함수(loss function)들의 작동 원리는 데이터 공간을 통계적으로 해석해서 유도하게 된다 에측이 틀릴 위험(risk)을 최소화하도록 데이터를 학습하는 원리는 통계적 기계학습의 기본 원리 회귀 분석에서 손실함수로 사용되는 L2-norm은 예측오차의 분산을 가장 최소화하는 방향으로 학습을 유도한다 분류 문제에서 사용되는 교차엔트로피(cross-entropy)는 모델 예측의 불확실성을 최소화하는 방향으로 학습하도록 유도 즉, data가 관찰된 분포 ↔ model 예측 분포 차이를 최소화하고자 한다 분산 및 불확실성을 최소화하기 위해서는 측정하는 방법을 알아야 한다 두 대상을 측정하는 방법을 통계학에서 제..
[05] 딥러닝 학습방법 이해하기 신경망 Neural Network 비선형모델인 신경망(neural network) 선형 모델이 숨겨져있다 선형모델 + 비선형 함수의 결합 선형 모델 O : output X : input data W : 가중치 행렬 b : y절편 데이터가 바뀌면 결과값도 바뀐다 출력 벡터 차원은 $d$에서 $p$로 바뀐다 $X$ (n x d) $\times$ W (d x p) → $O$ (n x p) $x_1 \Rightarrow o_1$ 화살표는 p개 softmax $$ softmax(o) = (\frac{exp(o_1)}{\sum_{k=1}^{p}exp(o_k)}, ...,\frac{exp(o_p)}{\sum_{p}^{k=1}exp(o_k)}) $$ 출력벡터 $o$에 softmax 함수를 합성하면 확률벡터가 되므로 특..
[04] 확률적 경사하강법 SGD 선형회귀분석 복습 역행렬을 이용하지 말고, 경사하강법을 이용해 적절한 선형모델을 찾아보자 선형모델 아닌 모델 → 경사하강법 사용 가능 경사하강법: 일반적인 기계학습 최적화 선형회귀의 목적식은 $\Vert y-X\beta \Vert_2$이고 (L2-norm) 이를 최소화하는 $\beta$를 찾아야 하므로 다음과 같은 gradient vector를 구해야 한다 $\nabla_\beta \Vert y-X\beta \Vert_2 = (\partial_{\beta_1} \Vert y-X\beta \Vert_2, ... , \partial_{\beta_d}\Vert y-X\beta \Vert_2)$ $\Vert y-X\beta \Vert_2$가 아닌 $\Vert y-X\beta \Vert_2^2$를 최소화해도 된다..
[03] 경사하강법 미분 Differentiation 미분(differentiation)은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구 최적화에서 제일 많이 사용하는 기법 미분은 변화율의 극한(limit)으로 정의 $f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$ 예시$f'(x) = 2x + 2$미분을 손으로 계산하려면 일일이 $h \rightarrow 0$ 극한을 계산해야 한다 $\frac{f(x+h) - f(x)}{h} = 2x + 2 + h$ $f(x) = x^2 + 2x + 3$ 최근에는, 미분을 손으로 직접 계산하는 대신 컴퓨터가 계산해준다! sympy.diff - symbolic python import sympy as sym from sympy.abc impor..
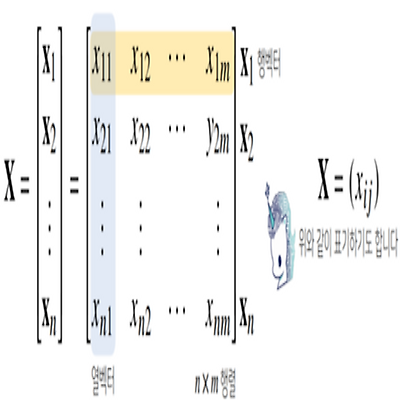
[02] 행렬 행렬이란? 행렬(matrix)는 벡터를 원소로 가지는 2차원 배열 벡터의 확장 벡터의 원소 → 숫자, 행렬의 원소 → 벡터 numpy에서는 행(row)이 기본 단위 x = np.array([1, -2, 3], [7, 5, 0], [-2, -1, 2]) 벡터 : 소문자 bold, 행렬 : 대문자 bold 행렬은 행(row)과 열(column)이라는 index를 가진다 $X = (x_{ij})$와 같이 표기하기도 한다 행렬의 특정 행(열)을 고정하면 행(열)벡터라고 부른다 전치행렬 (transpose matrix)은 행과 열의 인덱스가 바뀐 행렬 $X^T = (x_{ji})$ 행렬의 이해 (1) 벡터가 공간에서 한 점을 의미하면, 행렬은 여러 점들을 나타낸다 행렬의 행벡터 $x_i$는 i번째 데이터를 의미한..
[01] Vector Vector Vector 숫자를 원소로 가지는 list 또는 array 공간에서 한 점 (원점으로부터 상대적 위치) 표현 스칼라곱 시 방향은 그대로, 길이만 변함 두 벡터의 덧셈: 다른 벡터로부터 상대적 위치 이동 벡터의 노름(norm) 원점에서부터의 거리 L1 norm $\Vert x \Vert_1 = \sum_{i=1}^{d}\Vert x_i \Vert$ 각 성분의 변화량의 절대값의 합 robust 학습, lasso 회귀 L2 norm $\Vert x \Vert_2 = \sqrt{\sum_{i=1}^{d} \vert x_i \vert^2}$ 피타코갈스 정리를 이용해 유클리드 거리 계산 laplace 근사, ridge 회귀 두 벡터 사이의 거리 $\Vert y - x \Vert = \Vert x - ..

티스토리툴바